2.3.4 Types
Section §2.3.2 described
nine kinds of values.
Each kind of value is captured by a descriptor called a
In addition to the nine types, a tenth type – unknown – is produced when the type system fails to identify a type. The unknown type will only appear in an error message. Moreover, reals are subtyped internally as boolean, integer, decimal and complex-j to simplify the task of applying operators. The real subtypes are completely transparent to the user.
Myron associates a type with each variable, parameter, function and operator. The type of a variable or function is given by its type decoration which can be provided explicitly or inferred from the type of its elaboration. The type of an operator (or more formally, the type of the result produce by applying an operator to its operands) depends on the nature of the operator and the types of its operand(s). Some operators are defined to produce a particular result type regardless of operand type; others are defined to produce a type that depends on the operand types.
The order of the type list is important because it is used to determine the type of an operator when its operands have mixed types. The real type is said to be at the “low” end of the list and the string type is at the “high” end. This allows us to talk about the relative order of types and say that one type is lower or higher than another.
Values can be transformed to other types.
When a type transformation is applied explicitly, it is called a
The general rule for binary operators with mixed-type operands is to
coerce
the operand with lower type to that of the higher type.
For example, the complex operand in 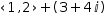
The cast operator is any of the formal or keyboard type notations
used as a postfix operator.
For example, if addition of a row vector and complex value is required to produce a complex result,
the row vector must be transformed using the ⅈ postfix cast operator:
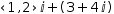
When type transformation takes a lower type to a higher type, it is called a
When narrowing would cause loss of information, the transformation fails. This is apparent in the workspace when simplification of a cast expression makes no change. Narrowings can be forced by casting first to tuple. For example, casting a 3-component vector to complex is not permitted, but casting from a 3-element tuple discards the third element. Requiring the intermediate tuple prevents inadvertent errors and requires the user to think about the transformation. Item-loss aside, casting from collection to composite also fails if the collection contains non-scalar elements.
Type transformation involving sets can also cause loss of information, even when widening.
For example, vectors
can contain more than one component with the same value. Widening
to a set causes duplicate elements to be discarded.
Because of this, composites cannot be cast to sets; rather
an intermediate widening to tuple is required, followed by a narrowing from
tuple to set. That is, (1,1)v s is illegal
but 
Casting to a string creates a string with the parsable representation of the operand. Casting from a string to any other type parses the string to produce the expression represented by the string, then casts that expression to the desired type.
The type of a unary operator is generally the type of its operand
except where the operator is defined to always result in a particular type.
When a unary operator is distributed across components of composite
types and elements of collection types, the resulting expression still has
the same type.
For example, the type of 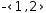

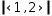
Although the higher-type rule for binary operators is attractive in its simplicity, there are several exceptions. Mixing tuples and sets with other operands uses elaborate coercion rules, described in §6.2.1. Other exceptions include the containment operator, which always returns a real result. Other operators that return a real from non-real operands are the set-test operators: subset, proper subset, superset, proper superset.
Set operations intersection, union and difference are also exceptions. For set and tuple operands, the higher-type rule applies. (Under set operations, tuples implement multisets.) However, if one of the operands is neither set nor tuple, the latter is promoted to a singleton of the former.
Multiplication is another exception. A special multiplication operator is used when the operands are composite or matrix. For radial and vector operands, multiplication produces the dot product, returning a scalar. The dot product is computed similarly to the matrix product of a 1-row matrix with a 1-column matrix except the result of the latter is a 1-row 1-column matrix instead of a scalar.
Although all of this seems unnecessarily complicated, there are
several reasons for having a type system in Myron. Foremost, checking types
when an expression is parsed reduces the number of situations in which types
will be incompatible when simplified or transformed. In addition, the type
system reduces the potential for mathematically meaningless expressions.
For example, the equation 
With the type system comes the expectation that no transformation will change the type of an expression. This is required to maintain the balance of equations and definitions with respect to type. To this end, transform expressions have the requirement that the pattern and replacement have the same type. This is already the case for substitution rules, which begin life as equations and are type checked by the parser.